Knapsack problem
The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. It derives its name from the problem faced by someone who is constrained by a fixed-size knapsack and must fill it with the most useful items.
The problem often arises in resource allocation with financial constraints. A similar problem also appears in combinatorics, complexity theory, cryptography and applied mathematics.
The decision problem form of the knapsack problem is the question "can a value of at least V be achieved without exceeding the weight W?"
Contents |
Definition
In the following, we have n kinds of items, 1 through n. Each kind of item i has a value vi and a weight wi. We usually assume that all values and weights are nonnegative. To simplify the representation, we can also assume that the items are listed in increasing order of weight. The maximum weight that we can carry in the bag is W.
The most common formulation of the problem is the 0-1 knapsack problem, which restricts the number xi of copies of each kind of item to zero or one. Mathematically the 0-1-knapsack problem can be formulated as:
- maximize
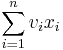
- subject to
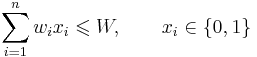
The bounded knapsack problem restricts the number  of copies of each kind of item to a maximum integer value
of copies of each kind of item to a maximum integer value 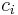 . Mathematically the bounded knapsack problem can be formulated as:
. Mathematically the bounded knapsack problem can be formulated as:
- maximize
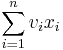
- subject to
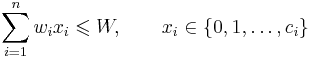
The unbounded knapsack problem (UKP) places no upper bound on the number of copies of each kind of item.
Of particular interest is the special case of the problem with these properties:
- it is a decision problem,
- it is a 0-1 problem,
- for each kind of item, the weight equals the value:
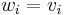 .
.
Notice that in this special case, the problem is equivalent to this: given a set of nonnegative integers, does any subset of it add up to exactly W? Or, if negative weights are allowed and W is chosen to be zero, the problem is: given a set of integers, does any nonempty subset add up to exactly 0? This special case is called the subset sum problem. In the field of cryptography, the term knapsack problem is often used to refer specifically to the subset sum problem.
If multiple knapsacks are allowed, the problem is better thought of as the bin packing problem.
Computational complexity
The knapsack problem is interesting from the perspective of computer science because
- there is a pseudo-polynomial time algorithm using dynamic programming
- there is a fully polynomial-time approximation scheme, which uses the pseudo-polynomial time algorithm as a subroutine
- the problem is NP-complete to solve exactly, thus it is expected that no algorithm can be both correct and fast (polynomial-time) on all cases
- many cases that arise in practice, and "random instances" from some distributions, can nonetheless be solved exactly.
The subset sum version of the knapsack problem is commonly known as one of Karp's 21 NP-complete problems.
There have been attempts to use subset sum as the basis for public key cryptography systems, such as the Merkle-Hellman knapsack cryptosystem. These attempts typically used some group other than the integers. Merkle-Hellman and several similar algorithms were later broken, because the particular subset sum problems they produced were in fact solvable by polynomial-time algorithms.
One theme in research literature is to identify what the "hard" instances of the knapsack problem look like,[1][2] or viewed another way, to identify what properties of instances in practice might make them more amenable than their worst-case NP-complete behaviour suggests.[3]
Several algorithms are freely available to solve knapsack problems, based on dynamic programming approach,[4] branch and bound approach[5] or hybridizations of both approaches.[3][6][7][8]
Dynamic programming solution
Unbounded knapsack problem
If all weights (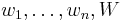 ) are nonnegative integers, the knapsack problem can be solved in pseudo-polynomial time using dynamic programming. The following describes a dynamic programming solution for the unbounded knapsack problem.
) are nonnegative integers, the knapsack problem can be solved in pseudo-polynomial time using dynamic programming. The following describes a dynamic programming solution for the unbounded knapsack problem.
To simplify things, assume all weights are strictly positive (wi > 0). We wish to maximize total value subject to the constraint that total weight is less than or equal to W. Then for each w ≤ W, define m[w] to be the maximum value that can be attained with total weight less than or equal to w. m[W] then is the solution to the problem.
Observe that m[w] has the following properties:
![m[0]=0\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/ece37db2427459763955834381136a84.png) (the sum of zero items, i.e., the summation of the empty set)
(the sum of zero items, i.e., the summation of the empty set)![m[w]= \max_{w_i \le w}(v_i%2Bm[w-w_i])](/2012-wikipedia_en_all_nopic_01_2012/I/639a8c4e9056cd0402e3fef9cbac56d6.png)
where 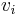 is the value of the i-th kind of item.
is the value of the i-th kind of item.
Here the maximum of the empty set is taken to be zero. Tabulating the results from ![m[0]](/2012-wikipedia_en_all_nopic_01_2012/I/5d506c9110bdf5f64cbc61d65fb8cb06.png) up through
up through ![m[W]](/2012-wikipedia_en_all_nopic_01_2012/I/8afec71f3cebff8a6340c67f15aab4cc.png) gives the solution. Since the calculation of each
gives the solution. Since the calculation of each ![m[w]](/2012-wikipedia_en_all_nopic_01_2012/I/2998e2124b58268125618f4aa3790514.png) involves examining
involves examining  items, and there are
items, and there are  values of
values of ![m[w]](/2012-wikipedia_en_all_nopic_01_2012/I/2998e2124b58268125618f4aa3790514.png) to calculate, the running time of the dynamic programming solution is
to calculate, the running time of the dynamic programming solution is 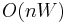 . Dividing
. Dividing  by their greatest common divisor is an obvious way to improve the running time.
by their greatest common divisor is an obvious way to improve the running time.
The 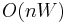 complexity does not contradict the fact that the knapsack problem is NP-complete, since
complexity does not contradict the fact that the knapsack problem is NP-complete, since  , unlike
, unlike  , is not polynomial in the length of the input to the problem. The length of the
, is not polynomial in the length of the input to the problem. The length of the  input to the problem is proportional to the number of bits in
input to the problem is proportional to the number of bits in  ,
, 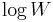 , not to
, not to  itself.
itself.
0-1 knapsack problem
A similar dynamic programming solution for the 0-1 knapsack problem also runs in pseudo-polynomial time. As above, assume  are strictly positive integers. Define
are strictly positive integers. Define ![m[i,w]](/2012-wikipedia_en_all_nopic_01_2012/I/5a8eab40d97b8f81718de6dce56307ee.png) to be the maximum value that can be attained with weight less than or equal to
to be the maximum value that can be attained with weight less than or equal to  using items up to
using items up to  .
.
We can define ![m[i,w]](/2012-wikipedia_en_all_nopic_01_2012/I/5a8eab40d97b8f81718de6dce56307ee.png) recursively as follows:
recursively as follows:
![m[0,\,w]=0](/2012-wikipedia_en_all_nopic_01_2012/I/d806129103dc968dd03cf45517240191.png)
![m[i,\,0]=0](/2012-wikipedia_en_all_nopic_01_2012/I/ea6a0e0fffef5a688c41efc4ea133e61.png)
![m[i,\,w]=m[i-1,\,w]](/2012-wikipedia_en_all_nopic_01_2012/I/cba5389c96e82ea7b3f6e6933afb92f0.png) if
if 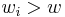 (the new item is more than the current weight limit)
(the new item is more than the current weight limit)![m[i,\,w]=\max(m[i-1,\,w],\,m[i-1,w-w_i]%2Bv_i)](/2012-wikipedia_en_all_nopic_01_2012/I/623ec5520b4cfa6fed8b0eac34eee5b4.png) if
if 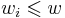 .
.
The solution can then be found by calculating ![m[n,W]](/2012-wikipedia_en_all_nopic_01_2012/I/4c984e5e6b255700ce8397efb693daee.png) . To do this efficiently we can use a table to store previous computations. This solution will therefore run in
. To do this efficiently we can use a table to store previous computations. This solution will therefore run in 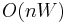 time and
time and 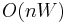 space. Additionally, if we use only a 1-dimensional array
space. Additionally, if we use only a 1-dimensional array ![m[w]](/2012-wikipedia_en_all_nopic_01_2012/I/2998e2124b58268125618f4aa3790514.png) to store the current optimal values and pass over this array
to store the current optimal values and pass over this array 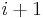 times, rewriting from
times, rewriting from ![m[W]](/2012-wikipedia_en_all_nopic_01_2012/I/8afec71f3cebff8a6340c67f15aab4cc.png) to
to ![m[1]](/2012-wikipedia_en_all_nopic_01_2012/I/c3a489b7e47d8b726a5643c2266f9f78.png) every time, we get the same result for only
every time, we get the same result for only 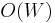 space.
space.
Another algorithm for 0-1 knapsack, discovered in 1974 [9] and sometimes called "meet-in-the-middle" due to parallels to a similarly-named algorithm in cryptography, is exponential in the number of different items but may be preferable to the DP algorithm when  is large compared to n. In particular, if the
is large compared to n. In particular, if the 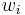 are nonnegative but not integers, we could still use the dynamic programming algorithm by scaling and rounding (i.e. using fixed-point arithmetic), but if the problem requires
are nonnegative but not integers, we could still use the dynamic programming algorithm by scaling and rounding (i.e. using fixed-point arithmetic), but if the problem requires  fractional digits of precision to arrive at the correct answer,
fractional digits of precision to arrive at the correct answer,  will need to be scaled by
will need to be scaled by 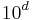 , and the DP algorithm will require
, and the DP algorithm will require 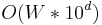 space and
space and 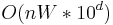 time.
time.
The "meet-in-the-middle" algorithm is as follows:
- Partition the set {1...n} into two sets A and B of approximately equal size
- Compute the weights and values of all subsets of each set.
- For each subset of A, find the "best matching" subset of B, i.e. the subset of B of greatest value such that the combined weight is less than W. Keep track of the greatest combined value seen so far.
The algorithm takes 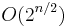 space, and efficient implementations of step 3 (for instance, sorting the subsets of B by weight, discarding subsets of B which weigh more than other subsets of B of greater or equal value, and using binary search to find the best match) result in a runtime of
space, and efficient implementations of step 3 (for instance, sorting the subsets of B by weight, discarding subsets of B which weigh more than other subsets of B of greater or equal value, and using binary search to find the best match) result in a runtime of 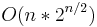 . As with the meet in the middle attack in cryptography, this improves on the
. As with the meet in the middle attack in cryptography, this improves on the 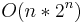 runtime of a naive brute force approach (examining all subsets of {1...n}), at the cost of using exponential rather than constant space.
runtime of a naive brute force approach (examining all subsets of {1...n}), at the cost of using exponential rather than constant space.
Greedy approximation algorithm
George Dantzig proposed a greedy approximation algorithm to solve the unbounded knapsack problem.[10] His version sorts the items in decreasing order of value per unit of weight, 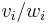 . It then proceeds to insert them into the sack, starting with as many copies as possible of the first kind of item until there is no longer space in the sack for more. Provided that there is an unlimited supply of each kind of item, if
. It then proceeds to insert them into the sack, starting with as many copies as possible of the first kind of item until there is no longer space in the sack for more. Provided that there is an unlimited supply of each kind of item, if  is the maximum value of items that fit into the sack, then the greedy algorithm is guaranteed to achieve at least a value of
is the maximum value of items that fit into the sack, then the greedy algorithm is guaranteed to achieve at least a value of 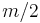 . However, for the bounded problem, where the supply of each kind of item is limited, the algorithm may be far from optimal.
. However, for the bounded problem, where the supply of each kind of item is limited, the algorithm may be far from optimal.
Dominance relations in the UKP
Solving the unbounded knapsack problem can be made easier by throwing away items which will never be needed. For a given item i, suppose we could find a set of items J such that their total weight is less than the weight of i, and their total value is greater than the value of i. Then i cannot appear in the optimal solution, because we could always improve any potential solution containing i by replacing i with the set J. Therefore we can disregard the i-th item altogether. In such cases, J is said to dominate i. (Note that this does not apply to bounded knapsack problems, since we may have already used up the items in J.)
Finding dominance relations allows us to significantly reduce the size of the search space. There are several different types of dominance relations,[3] which all satisfy an inequality of the form: 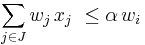 , and
, and 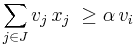 for some
for some 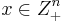
where 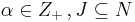 and
and 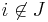 . The vector
. The vector  denotes the number of copies of each member of J.
denotes the number of copies of each member of J.
Collective dominance
The i-th item is collectively dominated by J, written as 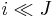 , if the total weight of some combination of items in J is less than wi and their total value is greater than vi. Formally,
, if the total weight of some combination of items in J is less than wi and their total value is greater than vi. Formally, 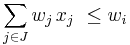 and
and 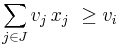 for some
for some 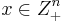 , i.e.
, i.e. 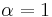 . Verifying this dominance is computationally hard, so it can only be used with a dynamic programming approach. In fact, this is equivalent to solving a smaller knapsack decision problem where2 V = vi, W = wi, and the items are restricted to J.
. Verifying this dominance is computationally hard, so it can only be used with a dynamic programming approach. In fact, this is equivalent to solving a smaller knapsack decision problem where2 V = vi, W = wi, and the items are restricted to J.
Threshold dominance
The i-th item is threshold dominated by J, written as 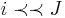 , if some number of copies of i are dominated by J. Formally,
, if some number of copies of i are dominated by J. Formally, 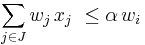 , and
, and 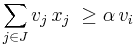 for some
for some 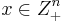 and
and 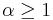 . This is a generalization of collective dominance, first introduced in[4] and used in the EDUK algorithm. The smallest such
. This is a generalization of collective dominance, first introduced in[4] and used in the EDUK algorithm. The smallest such  defines the threshold of the item i, written
defines the threshold of the item i, written 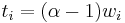 . In this case, the optimal solution could contain at most
. In this case, the optimal solution could contain at most 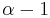 copies of i.
copies of i.
Multiple dominance
The i-th item is multiply dominated by a single item j, written as 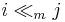 , if i is dominated by some number of copies of j. Formally,
, if i is dominated by some number of copies of j. Formally, 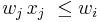 , and
, and 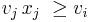 for some
for some 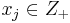 i.e.
i.e. 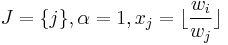 . This dominance could be efficiently used during preprocessing because it can be detected relatively easily.
. This dominance could be efficiently used during preprocessing because it can be detected relatively easily.
Modular dominance
Let b be the best item, i.e. 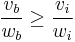 for all i. This is the item with the greatest density of value.
for all i. This is the item with the greatest density of value.
The i-th item is modularly dominated by a single item j, written as 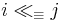 , if i is dominated by j plus several copies of b. Formally,
, if i is dominated by j plus several copies of b. Formally, 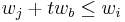 , and
, and 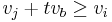 i.e.
i.e. 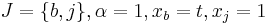 .
.
Applications
Knapsack problems can be applied to real-world decision-making processes in a wide variety of fields, such as the finding the least wasteful cutting of raw materials,[11] selection of capital investments and financial portfolios,[12] selection of assets for asset-backed securitization,[13] and generating keys for the Merkle–Hellman knapsack cryptosystem.[14]
One early application of knapsack algorithms was in the construction and scoring of tests in which the test-takers have a choice as to which questions they answer. On tests with a homogeneous distribution of point values for each question, it is a fairly simple process to provide the test-takers with such a choice. For example, if an exam contains 12 questions each worth 10 points, the test-taker need only answer 10 questions to achieve a maximum possible score of 100 points. However, on tests with a heterogeneous distribution of point values—that is, when different questions or sections are worth different amounts of points— it is more difficult to provide choices. Feuerman and Weiss proposed a system in which students are given a heterogeneous test with a total of 125 possible points. The students are asked to answer all of the questions to the best of their abilities. Of the possible subsets of problems whose total point values add up to 100, a knapsack algorithm would determine which subset gives each student the highest possible score.[15]
History
The knapsack problem has been studied for more than a century, with early works dating as far back as 1897.[16] It is not known how the name "knapsack problem" originated, though the problem was referred to as such in the early works of mathematician Tobias Dantzig (1884–1956) , suggesting that the name could have existed in folklore before a mathematical problem had been fully defined.[17]
The quadratic knapsack problem was first introduced by Gallo, Hammer, and Simeone in 1960.[18]
A 1998 study of the Stony Brook University algorithms repository showed that, out of 75 algorithmic problems, the knapsack problem was the 18th most popular and the 4th most needed after kd-trees, suffix trees, and the bin packing problem.[19]
See also
Notes
- ^ Pisinger, D. 2003. Where are the hard knapsack problems? Technical Report 2003/08, Department of Computer Science, University of Copenhagen, Copenhagen, Denmark.
- ^ L. Caccetta, A. Kulanoot, Computational Aspects of Hard Knapsack Problems, Nonlinear Analysis 47 (2001) 5547–5558.
- ^ a b c Vincent Poirriez, Nicola Yanev, Rumen Andonov (2009) A Hybrid Algorithm for the Unbounded Knapsack Problem Discrete Optimization http://dx.doi.org/10.1016/j.disopt.2008.09.004
- ^ a b Rumen Andonov, Vincent Poirriez, Sanjay Rajopadhye (2000) Unbounded Knapsack Problem : dynamic programming revisited European Journal of Operational Research 123: 2. 168–181 http://dx.doi.org/10.1016/S0377-2217(99)00265-9
- ^ S. Martello, P. Toth, Knapsack Problems: Algorithms and Computer Implementation, John Wiley and Sons, 1990
- ^ S. Martello, D. Pisinger, P. Toth, Dynamic programming and strong bounds for the 0-1 knapsack problem , Manag. Sci., 45:414–424, 1999.
- ^ G. Plateau, M. Elkihel, A hybrid algorithm for the 0-1 knapsack problem, Methods of Oper. Res., 49:277–293, 1985.
- ^ S. Martello, P. Toth, A mixture of dynamic programming and branch-and-bound for the subset-sum problem, Manag. Sci., 30:765–771
- ^ Horowitz, Ellis; Sahni, Sartaj (1974), "Computing partitions with applications to the knapsack problem", Journal of the Association for Computing Machinery 21: 277–292, doi:10.1145/321812.321823, MR0354006
- ^ George B. Dantzig, Discrete-Variable Extremum Problems, Operations Research Vol. 5, No. 2, April 1957, pp. 266–288, DOI: http://dx.doi.org/10.1287/opre.5.2.266
- ^ Kellerer, Pferschy, and Pisinger 2004, p. 449
- ^ Kellerer, Pferschy, and Pisinger 2004, p. 461
- ^ Kellerer, Pferschy, and Pisinger 2004, p. 465
- ^ Kellerer, Pferschy, and Pisinger 2004, p. 472
- ^ Feuerman, Martin; Weiss, Harvey (April 1973). "A Mathematical Programming Model for Test Construction and Scoring". Management Science 19 (8): 961–966. JSTOR 2629127.
- ^ Mathews, G. B. (25 June 1897). "On the partition of numbers". Proceedings of the London Mathematical Society 28: 486–490. http://plms.oxfordjournals.org/content/s1-28/1/486.full.pdf.
- ^ Kellerer, Pferschy, and Pisinger 2004, p. 3
- ^ Gallo, G.; Hammer, P. L.; Simeone, B. (1980). "Quadratic knapsack problems". Mathematical Programming Studies 12: 132–149. doi:10.1007/BFb0120892. http://www.springerlink.com/content/x804231403086x51/.
- ^ Skiena, S. S. (September 1999). "Who is Interested in Algorithms and Why? Lessons from the Stony Brook Algorithm Repository". AGM SIGACT News 30 (3): 65–74. ISSN 0163-5700. http://delivery.acm.org/10.1145/340000/333627/p65-skiena.pdf?key1=333627&key2=9434996821&coll=GUIDE&dl=GUIDE&CFID=108583297&CFTOKEN=90100478.
References
- Garey, Michael R.; David S. Johnson (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman. ISBN 0-7167-1045-5. A6: MP9, pg.247.
- Kellerer, Hans; Pferschy, Ulrich; Pisinger, David (2004). Knapsack Problems. Springer. ISBN 3-540-40286-1. MR2161720.
- Martello, Silvano; Toth, Paolo (1990). Knapsack problems: Algorithms and computer interpretations. Wiley-Interscience. ISBN 0-471-92420-2. MR1086874.
External links
- Lecture slides on the knapsack problem
- PYAsUKP: Yet Another solver for the Unbounded Knapsack Problem, with code taking advantage of the dominance relations in an hybrid algorithm, benchmarks and downloadable copies of some papers.
- Home page of David Pisinger with downloadable copies of some papers on the publication list (including "Where are the hard knapsack problems?")
- Knapsack Problem solutions in many languages at Rosetta Code
- Dynamic Programming algorithm to 0/1 Knapsack problem
- 0-1 Knapsack Problem in Python
- Interactive JavaScript branch-and-bound solver
- Solving 0-1-KNAPSACK with Genetic Algorithms in Ruby